1. 큐의 정의와 구현
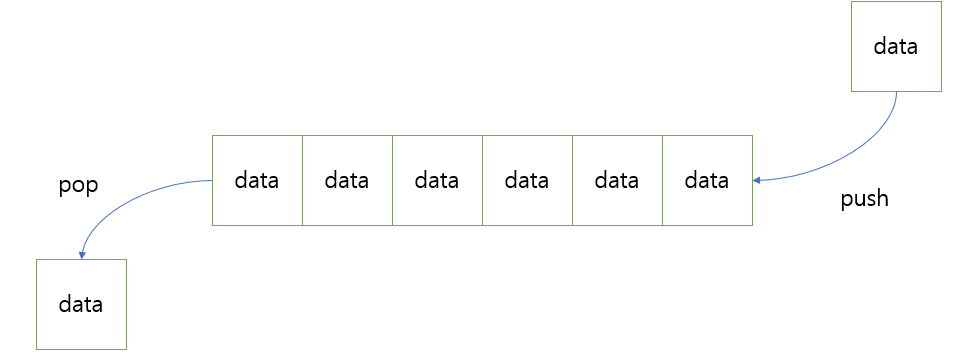
- Queue는 여러 게임(특히 대표적으로 롤)을 하면서 접할 수 있는 선착순의 개념이 적용된 자료구조이다. 즉 먼저 온 데이터가 먼저 나가는 FIFO(First-In-First-Out)의 구조를 가지고 있다.
- 이전에 배웠던 Stack이 tail에서 데이터의 삽입과 삭제가 수행되었다면, Queue는 데이터의 삽입은 Tail에서 이루어지고 삭제는 head에서 이루어진다.
- Queue 역시 배열과 연결 리스트로 구현이 가능하다. 일반적으로 배열보다는 연결 리스트를 더 선호하며 필자도 연결리스트로 구현하려고 한다.

2. 큐의 연산과 그 구현
- Queue의 연산들은 다음과 같다.
- 데이터의 삽입
- 데이터의 삭제
- 데이터의 조회(head 부분만)
- 큐의 상태와 길이
- 필자는 연결 리스트로 구현하기 때문에 Node 클래스가 당연히 들어가야한다. 이번에는 이전에 배운 단방향 연결 리스트가 아닌 양방향 연결 리스트를 구현하여 큐에 사용할 것이다.
- 데이터의 삽입이 tail에서 일어나기 때문에 양방향 연결 리스트를 사용하는게 시간 면에서 이득이다. 단방향 연결 리스트에서 삽입 연산은 O(N)이나 양방향은 O(1)에 해결이 가능하기 때문이다.
- 양방향은 노드의 다음 노드를 가리키는 next를 가지고 있을 뿐 아니라 이전 노드를 가리키는 prev도 가지고 있다.
class Node{
int data;
Node prev;
Node next;
Node(int data){
this.data = data;
this.prev = null;
this.next = null;
}
}- 또한 큐를 구현하기 위해 필요한 연산들을 미리 정의하였다. 이번에는 노드 풀 기법을 사용하지 않고 하도록 하겠다.
class DoubleLinkedList{
Node head;
Node tail;
int length;
DoubleLinkedList(){
head = new Node(-1);
head.next = null;
head.prev = null;
tail = new Node(-1);
tail.next = null;
tail.prev = null;
length = 0;
}
public void addLast(int data){
}
public int removeFirst(){
}
public int peekFirst(){
}
public int getLength(){
}
public boolean isEmpty(){
}
public String toString(){
}
}
3. 큐의 데이터 삽입 연산
- 큐에서 데이터의 삽입은 tail에서 일어난다. 즉 연결 리스트의 맨 마지막에서 수행된다.
- 이는 곧 연결 리스트에서 맨 마지막에 데이터를 삽입하는 연산과 동치이다. 다만 양방향 연결 리스트이기 때문에 단방향 연결 리스트에서 삽입하는 것보다 몇 가지 코드가 더 추가된다.
- 데이터 삽입을 할 때 다음의 경우의 수를 고려해야 한다.
- 연결 리스트가 비어있을 경우 즉, 큐가 비어있을 경우이다.
- 연결리스트가 비어있지 않을 경우
- 연결 리스트가 비어있을 경우, 삽입되는 데이터가 처음이자 마지막이 되므로 head 부분도 추가적으로 수정할 필요가 있다. 방법은 간단한데 head와 tail이 새로 삽입될 노드인 newNode를 가리키도록 하면 된다.
- 연결 리스트가 비어있지 않은 경우에는 맨 마지막 노드를 가리키는 tail을 이용하여 노드를 삽입한다.
public void addLast(int data){
Node newNode = new Node(data);
if (tail.prev == null){
head.next = newNode;
newNode.prev = head;
newNode.next = tail;
tail.prev = newNode;
} else{
newNode.next = tail;
newNode.prev = tail.prev;
tail.prev.next = newNode;
tail.prev = newNode;
}
length++;
}- 연결 리스트 구현을 수행하면서 그림을 그려 생각해보면 왜 이렇게 되는지 확실히 이해할 수 있을 것이다.
4. 큐의 데이터 삭제 연산
- 큐에서 데이터의 삭제 연산은 head에서 이루어진다.
- 이는 곧 연결 리스트에서 head에서 삭제 연산이 수행되는 것과 동치이며 양방향 연결 리스트임을 고려하여 구현하면 된다.
- 이때 큐가 비어있다면 해당 연산을 무시하도록 먼저 조치하는 것이 필요하다.
- 삭제 연산도 역시 단방향 연결 리스트와 동일하게 head의 next가 삭제되는 노드의 next를 가리키게 하고 삭제되는 노드의 next에 존재하는 노드의 이전 노드를 가리키는 prev가 head를 가리키도록 하면 된다.
public int removeFirst(){
int ret = -1;
if (head.next == null || head.next == tail){
return -1;
}
ret = head.next.data;
head.next.next.prev = head;
head.next = head.next.next;
length--;
return ret;
}
5. 큐의 나머지 부가 연산
- 큐의 길이 또는 상태체크와 큐의 요소 조회, 출력 기능은 다음과 같다.
public int peekFirst(){
return head.next.data;
}
public int getLength(){
return this.length;
}
public boolean isEmpty(){
return this.length == 0;
}
public String toString(){
StringBuilder sb = new StringBuilder();
Node start = head.next;
while(start.next != null){
sb.append(start.data);
sb.append(" ");
start = start.next;
}
return sb.toString();
}- 큐의 요소 조회(peek)은 head에서 진행되는것에 유의하자.
- 요소 조회는 정방향으로 순회하며 출력하는 것이다. 역방향 출력을 하려면 tail에서 prev를 타고 내려가게 하면 된다. 해보고 싶다면 구조는 위와 동일하니 한번 해보도록 하자.
6. 정리
- 큐나 스택, 그리고 다음에 살펴볼 덱(Deque)의 경우 단방향 연결 리스트로도 구현이 가능하지만 양방향 연결 리스트를 사용하면 입 출력에 대해 많은 시간적 이득을 가져갈 수 있다. 완벽히 구현할 필요도 없이 양 끝단에서 데이터의 삽입과 삭제 연산만 구현할 수 있으면 된다.
- 큐의 종류 중 우선순위 큐(Priority Queue)라는 자료구조가 존재하는데 이는 우선순위를 매겨 들어온 순서와 상관없이 우선순위가 가장 높은 데이터가 먼저 나가는 구조로 되어있다. 해당 자료구조는 선형 자료구조는 아니며 힙 이라는 특정 자료구조를 사용하여 구현한다.
- 큐의 전체 구현 코드와 테스트 코드는 다음과 같다.
class Node{
int data;
Node prev;
Node next;
Node(int data){
this.data = data;
this.prev = null;
this.next = null;
}
}
class Queue{
Node head;
Node tail;
int length;
Queue(){
head = new Node(-1);
head.next = null;
head.prev = null;
tail = new Node(-1);
tail.next = null;
tail.prev = null;
length = 0;
}
public void addFirst(int data){
Node newNode = new Node(data);
if (head.next == null){
head.next = newNode;
newNode.prev = head;
newNode.next = tail;
tail.prev = newNode;
} else{
newNode.next = head.next;
head.next.prev = newNode;
head.next = newNode;
newNode.prev = head;
}
length++;
}
public void addLast(int data){
Node newNode = new Node(data);
if (tail.prev == null){
head.next = newNode;
newNode.prev = head;
newNode.next = tail;
tail.prev = newNode;
} else{
newNode.next = tail;
newNode.prev = tail.prev;
tail.prev.next = newNode;
tail.prev = newNode;
}
length++;
}
public int removeFirst(){
int ret = -1;
if (head.next == null || head.next == tail){
return -1;
}
ret = head.next.data;
head.next.next.prev = head;
head.next = head.next.next;
length--;
return ret;
}
public int removeLast(){
int ret = -1;
if (tail.prev == null || tail.prev == head){
return -1;
}
ret = tail.prev.data;
tail.prev.prev.next = tail;
tail.prev = tail.prev.prev;
length--;
return ret;
}
public int peekFirst(){
return head.next.data;
}
public int peekLast(){
return tail.prev.data;
}
public int getLength(){
return this.length;
}
public boolean isEmpty(){
return this.length == 0;
}
public String toString(){
StringBuilder sb = new StringBuilder();
Node start = head.next;
while(start.next != null){
sb.append(start.data);
sb.append(" ");
start = start.next;
}
return sb.toString();
}
}
public class MyQueue {
public static void main(String[] args){
Queue myList = new Queue();
myList.addFirst(1);
myList.addFirst(2);
myList.addFirst(3);
myList.addFirst(4);
myList.addFirst(5);
System.out.println(myList + " " + myList.getLength());
myList.addLast(2);
myList.addLast(3);
myList.addLast(4);
myList.addLast(5);
System.out.println(myList + " " + myList.getLength());
myList.removeFirst();
myList.removeFirst();
myList.removeLast();
myList.removeLast();
System.out.println(myList + " " + myList.getLength());
}
}'DataStructure > List' 카테고리의 다른 글
| Stack의 활용 - VPS (0) | 2023.03.06 |
|---|---|
| 덱(deque)의 정의와 구현 (0) | 2023.02.23 |
| Stack의 구현 (0) | 2023.02.20 |
| LinkedList의 구현 - Single Linked List (0) | 2023.02.20 |
| LinkedList의 구현 - Single Linked List (0) | 2023.01.30 |