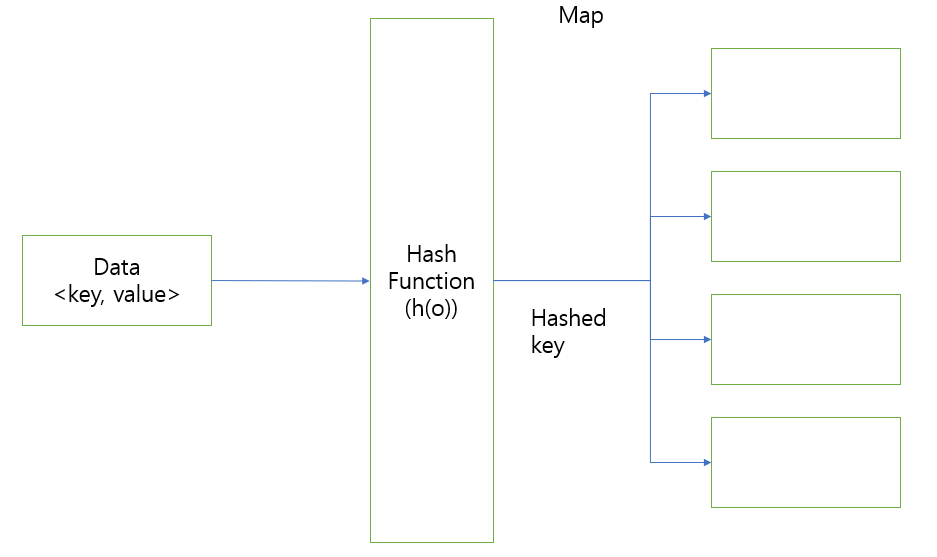
기본적인 용어의 정의
- Map부터 알아보자. 기본적으로 Map은 어떠한 데이터를 저장할 때 key와 value 쌍을 저장하는 자료구조로, 데이터를 Map 내부에서 탐색하거나 값을 참조하기 위해서는 key를 통해 접근해야 한다.
- 이를 조금 더 이해하기 쉽도록 생각하자면 배열에서 색인(index)을 통해 요소에 접근하는것 처럼, Map에서는 key를 통해 요소에 접근한다. 즉 기존 정수로만 제한되어 있던 색인을 정수 뿐만이 아닌 여러 타입으로 확장하였다고 생각하면 이해하기가 쉬울 것이다.
- Map의 특징으로는 key의 중복을 허용하지 않으며 대신 value의 중복은 허용된다. 또한 key를 통해 데이터의 접근, 탐색에 $O(1)$라는 강력한 성능을 가지는 것도 특징이다.
- Hash는 어떠한 데이터를 입력받은 후 특정한 수식에 의해 고정된 길이로 변형된 데이터를 출력하는 과정을 말한다. Hash라고도 하고 Hashing이라고도 한다.
- 해당 프로세스를 진행하는 함수(function)을 해시함수라고 하며 해당 함수의 특징은 들어오는 값의 길이는 다를 수 있으나 그 결과로 내보내는 데이터의 길이는 모두 고정적이라는 것이다.
- 또한 보안적 측면에서 결과로 내보낸 데이터를 다시 원본으로 복구하기가 매우 어려운 일방향 함수라는 특징도 가진다. 이를 이용하여 전자서명이나 블록체인등의 보안적 측면에서 사용되기도 한다.
HashMap
- 그렇다면 HashMap은 무엇일까? 위에서 설명한 용어를 조합한다면 해싱 함수를 사용하는것과 Map자료구조란 것을 알 수 있다.
- 실제로도 그러하며 Map자료구조이지만 key를 저장할 때, hashing을 사용하여 해시함수를 통과한 key를 저장한다.
- 이는 key를 통해 데이터를 탐색하는데 코스트가 적게 들도록 하는 방법이기도 하다. 만약 해싱을 하지 않은 raw key를 사용하여 데이터를 탐색해야 한다면 각 글자나, 객체를 비교하여 동일한지를 확인해야 하기 때문에 그에 대한 추가적인 코스트가 들겠지만, 이를 해싱으로 뭉게어 하나의 값으로 표현함으로서 비교에 대한 코스트가 절감된다.

- 하지만 해시함수를 통하여 키를 해싱하는 특성 상 하나의 문제점이 존재한다.
- 해시함수가 해싱을 통하여 내놓을 수 있는 값들은 무한하지 않다. 즉 낼 수 있는 최대한의 가짓수가 존재한다.
- 그렇다면 해시함수가 내놓을 수 있는 최대한의 해시 값 가짓수를 $H_{max}$라고 하자. 그렇다면 만약 입력으로 $H_{max} + 1$개의 key들이 들어온다면 비둘기집 원리에 의하여 반드시 중복되는 해시값이 존재한다.
- 이러한 경우가 발생하는 것을 "충돌"(collision)이라고 하며 충돌이 발생할 경우 전혀 다른 값을 가져올 수 있기 때문에 이에 대한 해결책을 마련해야 한다.
- 이에 대한 해결책으로는 Open Addressing과 Chaning이 있다.
Chaning
- 체이닝의 경우, 충돌이 발생한다면 키에 해당하는 값을 연결 리스트로 추가하는 방식이다.
- 충돌이 발생한 슬롯을 연결 리스트화 시켜 저장하기 때문에 충돌이 아무리 일어나도 동일한 키에 모두 저장이 가능하다. 대신 연결 리스트의 구조 상 최악의 경우에 데이터를 검색하는데 시간이 $O(N)$이 된다(모든 데이터가 충돌되어 하나의 연결 리스트로 들어가는 경우)
- 따라서 이러한 시간 코스트를 줄이기 위해 연결 리스트가 아닌 Tree를 이용하여 데이터를 저장하는 Chaining 방식도 있다.

Open Addressing
- Open Addressing은 충돌이 발생한 경우 해시함수로 얻은 주소 공간이 아닌 다른 주소 공간에 value를 저장한다.
- 그렇다면 저장할 다른 주소 공간을 어떻게 찾을 것인가를 또 논해볼 수 있다. 이는 3가지 방식으로 나뉜다.
- 첫 번째 방식으로 선형 프로빙이 있다.
- 선형 프로빙 방식의 경우 충돌이 발생하면 빈 공간을 찾을 때 까지 탐색을 수행한다. 이때 해시 함수는 아래의 해시 함수를 사용하게 된다.
- $h(k, i) = (h'(k) + i) mod (m)$
- 이때, k는 키, i는 충돌 횟수, m은 해시 테이블(저장공간)의 크기를 말한다.
- 선형 프로빙의 경우 구현의 간편함이 장점이나 한번 충돌이 발생할 경우, 위의 해시 함수를 그대로 따라가며 탐색을 진행하기 때문에 계속해서 충돌이 발생할 수 있다.
- 예를 들어 N개의 키가 모두 동일한 해시 값을 가짐으로 인해 충돌되어 선형 프로빙을 통해 저장되어 있을 때, 입력으로 들어온 다른 키가 다시 충돌이 발생한다면, N번의 충돌이 발생하게 되는 것이다.
- 또한 원래 존재해야 할 공간이 아닌 빈 공간을 빌려 쓰는 것이기 때문에 해당 빈 공간으로 해싱되어 들어온 데이터가 존재한다면 또 충돌이 발생하게 된다. 이를 Primary clustering이라고 한다.
- 두 번째 방식으로는 이차식 프로빙이 있다.
- 이차식 프로빙은 아래와 같은 해시 함수를 사용하는데, 충돌 카운터 i에 대한 2차 함수 꼴로 빈 공간을 탐색한다. 즉 충돌이 일어날 수록 더 멀리 떨어진 공간들을 탐색하여 빈 공간을 찾는 방식이다.
- $h(k, i) = (h'(k) + c_1i + c_2i) mod (m)$
- 해당 방식 역시 선형 프로빙처럼 충돌이 많이 발생했던 키로 데이터가 들어오면 연속해서 충돌이 발생하는 단점이 있다. 이를 secondary clustering이라고 한다.
- 마지막 방식으로는 이중 해시 방식이 있다.
- 이중 해싱은 충돌이 없을 때는 1번 해시 함수를 사용하고, 충돌이 있다면 2번 해시 함수를 통해 얻은 값을 해시 테이블의 크기로 나눈 나머지만큼 이동하면서 빈 공간을 탐색하게 된다.
정리
- Open Addressing의 성능은 일반적으로 Chaining을 택한 해시 테이블보다 성능이 좋다. 하지만 용량이 점점 차게 될 수록 충돌이 상대적으로 많이 일어나기 때문에 Open Addressing의 성능이 급격히 하락한다.
- Java의 경우에는 연결 리스트를 사용하는 Chaining 전략을 사용하고 있다.
- Java는 이전 Java 7(JDK 1.7)까지는 Seperate Chaining으로 연결 리스트를 사용하였으나 Java 8 (JDK 1.8)부터는 트리를 사용하여 Seperate Chaning을 사용하여 더 최적화 하였다고 한다.
- 이전에 사용하던 HashMap에서 get 메서드를 사용할 시 시간 복잡도의 기댓값은 $O(N/M)$ 이나 트리를 사용한 HashMap에서 get 메서드를 사용할 시 시간 복잡도의 기댓값은 $O(log(N/M))$이 된다. 해당 복잡도의 차이는 작은 데이터 크기에서는 무시가 가능한 수준이나 몇억, 몇십억 개의 데이터에서는 유의미한 성능을 보이는 것을 확인할 수 있다.
- Python의 경우 Dictionary라는 명칭으로 HashMap을 정의해 놓았으며 Open Addressing방식을 사용한다.
'DataStructure > Hash, map, set' 카테고리의 다른 글
| 프로그래머스 - 위장 (0) | 2023.03.16 |
|---|---|
| BOJ 26008 해시해킹 (0) | 2023.03.16 |
| Programmers - 압축 (0) | 2023.03.14 |
| Hash, map의 문제 유형 탐구 (0) | 2022.11.23 |