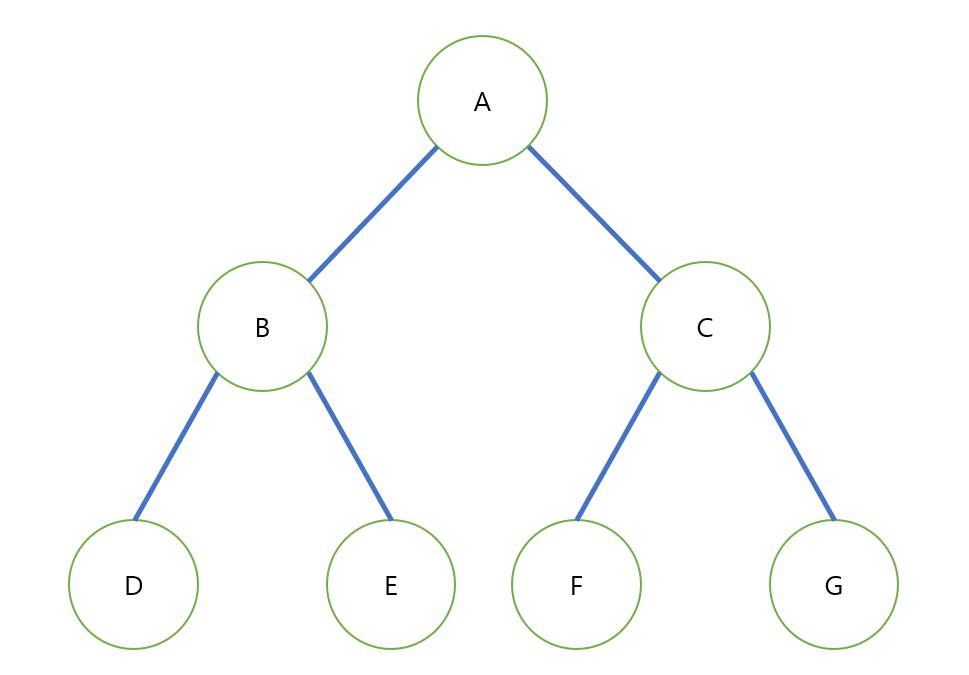

트리의 정의
- 트리의 정의는 그래프 이론에서 회로(Cycle)이 존재하지 않는 연결된 그래프로 정의한다.
- 여기서 회로 또는 사이클 이란 어떤 노드에서 시작하여 그 노드로 다시 되돌아가는 경로를 말한다.
- 일반적으로 위와 같이 어떠한 계층(hierarchy)을 이루는 구조를 말한다. 이것을 사용하는 가장 대표적인 예시가 조직도, 컴퓨터의 파일 시스템이다.
트리의 용어 설명
- 트리에서 자주 접할 수 있는 용어들은 루트, 부모, 자식, 레벨, 간선, 차수, 리프노드, 서브트리, 형제 노드가 있다.
- 루트 또는 루트 노드(root)란 트리의 시작점이 되는 노드를 말한다. 위 그림에서는 A가 루트 노드가 된다.
- 레벨(level)은 루트 노드부터 노드까지 연결된 간선수의 합으로 정의한다. 루트 노드 자신은 0 level이 되며 노드 B의 level은 1이 된다(간선이 1개이므로)
- 부모 노드(Parent)는 직접적으로 연결된 두 노드가 존재할 때 루트와 가까운 노드를 말한다.
- 자식 노드(Child)는 직접적으로 연결된 두 노드가 존재할 때 루트와 먼 노드를 말한다.
- 간선(Edge)은 두 노드를 연결시키는 링크를 말한다.
- 차수(degree)는 각 노드의 자식의 개수를 말한다. 트리의 차수(degree of tree)는 각 노드의 차수 중 최대값을 말한다.
- 리프 노드는 자식 노드를 가지지 않는 노드를 말한다. 단말(terminal) 노드라고도 한다.
- 서브트리는 트리 내부의 어떤 정점을 루트로 하는 부분적인 트리를 말한다.
- 형제 노드(brother)는 부모가 동일한 동일한 레벨의 두 노드를 말한다.
이진 트리의 정의와 종류
- 이진 트리(Binary Tree)는 모든 노드가 최대 2개의 자식만 가지는 트리를 말한다.
- 이진 트리의 종류는 정 이진 트리(Full Binary Tree), 포화 이진 트리(Perfect Binary Tree), 완전 이진 트리(Full Binary Tree)로 나누어진다.
- 정 이진 트리는 모든 트리의 자식이 0개 또는 2개로 구성된 이진 트리를 의미한다.
- 포화 이진 트리는 모든 리프노드의 높이가 동일하고, 리프 노드가 아닌 노드는 2개의 자식을 가진 노드로 구성된 이진 트리를 의미한다.
- 완전 이진 트리는 모든 리프노드의 높이 차이가 최대 1차이가 나고 우측 자식이 존재한다면 좌측 자식도 반드시 존재하는 이진 트리이다. 즉 좌측부터 우측으로 노드들을 순서대로 채우는 이진 트리를 의미한다.
- 위 사진의 이진 트리는 정 이진 트리인 동시에 포화 이진 트리이며 완전 이진 트리이기도 하다.
이진 트리의 순회
- 이진 트리에서의 순회(Traversal)은 전위, 중위, 후위의 3개 순회로 나누어진다.
- 전위 순회(pre-order traversal)은 자신 - 왼쪽 자식 - 오른쪽 자식으로 순회하는 순회 방식이다. 위 트리의 전위 순회는 A B D E C F G가 된다.
- 중위 순회(in-order traversal)은 왼쪽 자식 - 자신 - 오른쪽 자식으로 순회하는 순회 방식이다. 위 트리의 중위 순회는 D B E A F C G가 된다.
- 후위 순회(post-order traversal)은 왼쪽 자식 - 오른쪽 자식 - 자신으로 순회하는 순회 방식이다. 위 트리의 후위 순회는 D E B F G C A가 된다.
- 위 3가지 순회법과는 별개로 레벨 순회(level traversal)이 존재하는데 말 그대로 각 레벨에 있는 노드들을 좌에서 우로 하나씩 순회하는 방법이다. 위 트리에서 레벨 순회를 진행하면 A B C D E F G가 된다.
정리
- 이번에는 트리의 개념에 대해 간략히 정리하였다. 이제 정리한 개념을 토대로 트리를 직접 구현할 것이다.
- 트리의 구현 방식에는 2가지가 있으며 각각 배열과 연결 리스트를 사용한다. 두 가지 방식 모두 구현해볼 것이다.
'DataStructure > Tree' 카테고리의 다른 글
| AVL트리의 원리와 구현 (1) (0) | 2023.02.27 |
|---|---|
| 이진 탐색 트리의 원리와 구현 - (2) (0) | 2023.02.26 |
| 이진 탐색 트리의 원리와 구현 - (1) (0) | 2023.02.26 |
| 이진 트리의 구현 - (2) (0) | 2023.02.24 |
| 이진 트리의 구현 - (1) (0) | 2023.02.24 |