들어가며
- 이전 글에서 AVL트리가 어떻게 균형을 자동으로 수복하기 위해 수행하는 4가지 연산(LL, RR, LR, RL연산)에 대해 알아보았다.
- 이번에는 AVL 트리를 구현하면서 이전 글에서 본 4가지 연산이 어떻게 코드로 구현되는지에 대하여 알아본다.
- 또한 저번 이진 탐색 트리를 구현할 때 반복문을 통한 구현을 수행했는데 이번에는 재귀로도 구현하는 방법을 같이 알아본다.
AVL 트리의 구조
- AVL 트리는 자체적으로 균형을 유지하는것 이외에는 이진 탐색 트리와 동일하다. 따라서 사용자는 AVL 트리를 이진 탐색 트리를 사용하는 것 처럼 사용할 수 있으며 자체적으로 어떻게 균형이 유지되는가는 알지 못해도 상관없다.
- 따라서 자체적으로 균형을 맞추는 모든 연산과 균형의 상태, 높이의 연산따위의 정보는 모두 private로 진행되어도 관계없으며 데이터의 삽입 삭제 연산만 외부로 노출되도록 만들어야 할 것이다.
import java.util.*;
class Node{
int data;
int height;
Node left;
Node right;
Node(int data){
this.data = data;
this.left = null;
this.right = null;
this.height = 0;
}
}
class AVL_Tree {
Node root;
AVL_Tree(){
this.root = null;
}
private int getHeight(Node node){
}
private int getBalance(Node node){
}
private Node rightRotate(Node node){
}
private Node leftRotate(Node node){
}
private Node LR_Rotate(Node node){
}
private Node RL_Rotate(Node node){
}
public void addNode(int key){
}
private Node add(Node cur, int key){
}
public boolean searchNode(Node cur, int key){
}
public void removeNode(int key){
}
private Node remove(Node cur, int key){
}
public void levelTraversal(){
Deque<Node> queue = new ArrayDeque<>();
queue.addLast(this.root);
while (!queue.isEmpty()){
Node cur = queue.pollFirst();
System.out.print(cur.data + " ");
if (cur.left != null) queue.addLast(cur.left);
if (cur.right != null) queue.addLast(cur.right);
}
System.out.println();
}
public void traversal(Node cur){
if (cur == null){
return;
}
traversal(cur.left);
System.out.print(cur.data + " ");
traversal(cur.right);
}
}
- 이진 탐색 트리를 구현할 때와 같이 데이터의 존재 유무, 데이터의 삽입 삭제를 사용자에게 보이고 나머지는 접근할 수 없도록 구현할 것이다.
- level 순회의 경우 AVL트리가 정상적으로 동작하는지를 확인하기 위해 사용할 것이다.
균형 상태의 확인과 높이 확인
- 노드의 높이 정보를 노드 자체의 멤버로 두어 확인할 수 있게 하였다. 따라서 해당 정보를 그대로 반환하면 높이 확인의 부분은 종료된다.
- 균형 상태의 확인은 확인하고 싶은 노드의 좌측 노드의 높이와 우측 노드의 높이를 구하여 빼면 구할 수 있다. 이는 노드의 높이가 해당 노드를 루트로 하는 서브트리의 높이이기 때문이다.
- 이를 구현하면 다음과 같다.
private int getHeight(Node node){
if (node == null){
return -1;
}
return node.height;
}
private int getBalance(Node node){
if (node == null){
return 0;
}
return getHeight(node.left) - getHeight(node.right);
}
자가 수복 연산 - LL, RR 회전 연산
- LL, RR 회전 연산은 들어온 노드와 그 노드의 우측 또는 좌측 자식을 대상으로 회전하는 연산이다.
- LL연산을 예시로 들어보자 LL연산은 두 노드를 우측으로 회전시키는 연산이다. 이때 입력으로 받은 노드와 그 노드의 좌측 자식 노드가 우측 자식을 가진 경우도 고려해야 한다.
- 이 경우에 좌측 자식 도느의 우측 자식 노드를 입력으로 받은 노드의 좌측 자식으로 편입함으로서 연산을 진행할 수 있다.
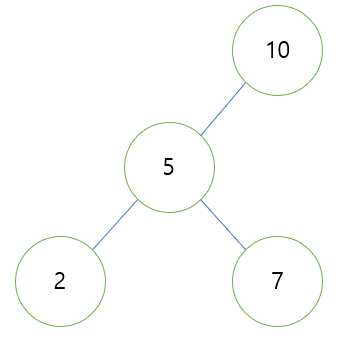예시 트리
- 위와 같은 트리가 있을 때 노드 10, 5를 LL 회전을 한다고 가정하자. 이때 5의 우측 자식으로 7이 존재한다.
- 이 우측 자식을 10의 좌측 자식으로 한다. 그럼 아래 그림과 같이 될 것이다.
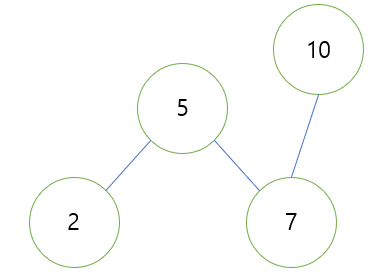링크 재설정
- 이후 5의 우측 자식을 7이 아닌 10으로 재설정함으로서 회전이 완료된다.
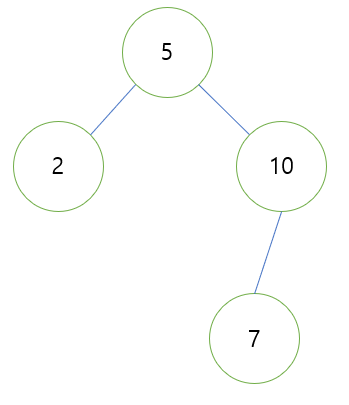회전 결과
// LL 회전
private Node rightRotate(Node node){
Node lNode = node.left;
node.left = lNode.right;
lNode.right = node;
node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
lNode.height = Math.max(getHeight(lNode.left), getHeight(lNode.right)) + 1;
return lNode;
}
// RR 회전
private Node leftRotate(Node node){
Node rNode = node.right;
node.right = rNode.left;
rNode.left = node;
node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
rNode.height = Math.max(getHeight(rNode.left), getHeight(rNode.right)) + 1;
return rNode;
}
- 링크를 재설정한 뒤 높이의 계산이 다시 이루어진다.
- 얼핏 보면 lNode.right의 높이가 왜 다시 계산되지 않는가라는 생각이 들 수 있다. 이는 위 그림을 보며 높이를 계산해보면 링크가 어떻게 설정되어도 높이가 변하지 않음을 알 수 있다. 따라서 계산할 필요가 없다.
- LL 회전의 구현이 완료되었다면 RR회전은 그 대칭으로만 구현하면 끝난다. 따로 설명할 것은 없기 때문에 RR 회전 연산까지 바로 구현하였다.
자가 수복 연산 - RL, LR회전 연산
- RL, LR 연산은 그 원리상 이미 구현된 LL, RR 회전 연산을 적절히 사용하는 것으로 구현이 가능하다.
- RL 연산은 LL연산을 수행한 뒤 RR 연산을 수행하여 구현할 수 있다. LR연산은 그 역으로 함으로서 구현이 가능하다.
- 이때 연산의 수행 대상을 잘 생각해야한다. 처음 수행되는 연산은 입력으로 들어온 노드가 대상이 아니라 입력으로 들어온 노드의 좌측 또는 우측 자식을 대상으로 하는 것이기 때문에 이를 유의하여 구현하여야 한다.
private Node LR_Rotate(Node node){
node.left = leftRotate(node.left);
return rightRotate(node);
}
private Node RL_Rotate(Node node){
node.right = rightRotate(node.right);
return leftRotate(node);
}
삽입 연산
- 이번에 이진 탐색 트리를 재귀로 구현하기로 하였다. 재귀를 통해 노드를 넣은 트리의 결과를 다시 루트에 적용시켜 트리 전체를 업데이트 해야하므로 입력단은 아래와 같을 것이다.
public void addNode(int key){
if (searchNode(this.root, key)){
return;
}
this.root = add(this.root, key);
}
- 이제 본격적인 삽입을 구현해 보자.
- 노드를 삽입하는 시점은 내가 현재 위치하는 곳이 null로 비어있는가 아닌가를 확인하고 비어있다면 새로운 노드를 그곳에 생성하여 반환하는 것이다.
- 만약 현재 위치하는 곳이 이미 노드가 존재하고 있다면 그 노드와 값을 비교하여 크다면 우측으로 작다면 좌측으로 이동해야한다.
- 여기까지 구현하면 다음과 같다.
private Node add(Node cur, int key){
if (cur == null){
return new Node(key);
}
if (cur.data < key){
cur.right = add(cur.right, key);
} else{
cur.left = add(cur.left, key);
}
cur.height = Math.max(getHeight(cur.left), getHeight(cur.right)) + 1;
return cur;
}
- 코드가 이해되지 않는다면 루트부터 시작해 함수를 타고 따라들어가보는 것을 추천한다.
- 이후 해당 노드의 높이를 재설정한다. 이는 삽입이 종료된 이후 재귀적으로 호출된 모든 노드들의 높이가 재설정된다. 그 말은 재귀호출에 사용된 모든 노드들이 벨런스 체크를 받아야 하고 문제가 존재한다면 위 연산을 통해 벨런스를 다시 맞춰야 한다는 것을 의미한다.
- 새로운 노드가 어디에 삽입되었는지는 삽입되는 데이터가 노드의 우측에 삽입되었는지 좌측에 삽입되었는지를 확인하여 알 수 있고, 벨런스가 -1보다 작은가 또는 1보다 큰가를 통해 트리가 어떻게 편향되었는지를 알 수 있다.
private Node add(Node cur, int key){
if (cur == null){
return new Node(key);
}
if (cur.data < key){
cur.right = add(cur.right, key);
} else{
cur.left = add(cur.left, key);
}
cur.height = Math.max(getHeight(cur.left), getHeight(cur.right)) + 1;
int balance = getBalance(cur);
if (balance > 1 && cur.data < key){
return LR_Rotate(cur);
}
if (balance > 1 && cur.data > key){
return rightRotate(cur);
}
if (balance < -1 && cur.data < key){
return leftRotate(cur);
}
if (balance < -1 && cur.data > key){
return RL_Rotate(cur);
}
return cur;
}
- balance > 1은 좌측 서브트리의 높이 - 우측 서브트리의 높이로 balance가 계산되는 특성상 좌측 서브트리가 편향되어 있다는 것을 의미한다. 이후 삽입된 노드의 위치가 좌측이냐 우측이냐에 따라 LL, LR 회전이 갈리게 된다.
- balance < -1은 역시 balance의 정의에 의해 우측 서브트리가 편향되어 있다는 것을 의미한다. 이후 삽입된 노드의 위치에 따라 RR, RL이 갈리게 된다.
정리
- 이번 글에서는 LL, LR, RL, RR 회전 연산의 구현과 AVL트리에서 노드의 삽입을 구현하였다. 다음 글에서는 AVL트리에서 노드의 삭제와 그때 일어날 수 있는 불균형에 대한 AVL트리의 대응 구현을 살펴본다.
- 지금까지 구현한 AVL트리의 코드들은 아래와 같다.
import java.util.*;
class Node{
int data;
int height;
Node left;
Node right;
Node(int data){
this.data = data;
this.left = null;
this.right = null;
this.height = 0;
}
}
class AVL_Tree {
Node root;
AVL_Tree(){
this.root = null;
}
private int getHeight(Node node){
if (node == null){
return -1;
}
return node.height;
}
private int getBalance(Node node){
if (node == null){
return 0;
}
return getHeight(node.left) - getHeight(node.right);
}
private Node rightRotate(Node node){
Node lNode = node.left;
node.left = lNode.right;
lNode.right = node;
node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
lNode.height = Math.max(getHeight(lNode.left), getHeight(lNode.right)) + 1;
return lNode;
}
private Node leftRotate(Node node){
Node rNode = node.right;
node.right = rNode.left;
rNode.left = node;
node.height = Math.max(getHeight(node.left), getHeight(node.right)) + 1;
rNode.height = Math.max(getHeight(rNode.left), getHeight(rNode.right)) + 1;
return rNode;
}
private Node LR_Rotate(Node node){
node.left = leftRotate(node.left);
return rightRotate(node);
}
private Node RL_Rotate(Node node){
node.right = rightRotate(node.right);
return leftRotate(node);
}
public void addNode(int key){
if (searchNode(this.root, key)){
return;
}
this.root = add(this.root, key);
}
private Node add(Node cur, int key){
if (cur == null){
return new Node(key);
}
if (cur.data < key){
cur.right = add(cur.right, key);
} else{
cur.left = add(cur.left, key);
}
cur.height = Math.max(getHeight(cur.left), getHeight(cur.right)) + 1;
int balance = getBalance(cur);
if (balance > 1 && cur.data < key){
return LR_Rotate(cur);
}
if (balance > 1 && cur.data > key){
return rightRotate(cur);
}
if (balance < -1 && cur.data < key){
return leftRotate(cur);
}
if (balance < -1 && cur.data > key){
return RL_Rotate(cur);
}
return cur;
}
public boolean searchNode(Node cur, int key){
}
public void removeNode(int key){
}
private Node remove(Node cur, int key){
}
public void levelTraversal(){
Deque<Node> queue = new ArrayDeque<>();
queue.addLast(this.root);
while (!queue.isEmpty()){
Node cur = queue.pollFirst();
System.out.print(cur.data + " ");
if (cur.left != null) queue.addLast(cur.left);
if (cur.right != null) queue.addLast(cur.right);
}
System.out.println();
}
public void traversal(Node cur){
if (cur == null){
return;
}
traversal(cur.left);
System.out.print(cur.data + " ");
traversal(cur.right);
}
}