들어가며
이전에 보았던 다익스트라는 하나의 정점에서 다른 정점까지의 모든 최단 경로를 구하는데 $O((V + E) \log V)$라는 강력한 성능을 보여주었다. 하지만 문제점이 있는데 음의 가중치가 존재하는 경우 제대로 된 값을 구할 수 없다는 것이다.
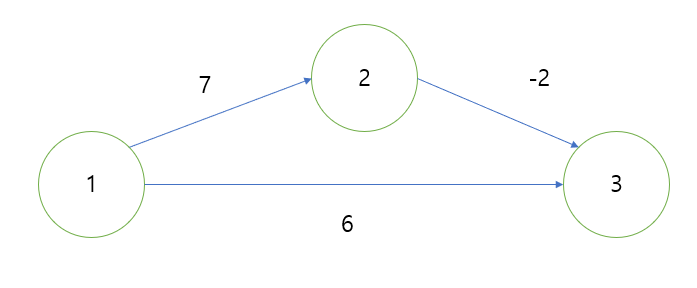
이는 그리디 알고리즘의 허점과도 연관되는데 아래와 같은 간단한 그래프를 통해 알아보자.
해당 그래프에서 1부터 시작한다고 가정할 때 최단 경로는 5가 된다.
하지만 다익스트라를 사용할 시 6이 되는데 그리디하게 1번과 인접한 곳의 가중치가 각각 7, 6으로 가중치가 더 적은 6을 먼저 갱신해버리기 때문이다.
이러한 문제를 해결하기 위해서는 이미 갱신해버린 값이어도 다시 한번 검사를 해보는 방식이 필요한데 이런 방식을 구현한 알고리즘이 Bellman-Ford 알고리즘이다.
Bellman - Ford 알고리즘의 원리
해당 알고리즘은 꽤 심플한 원리를 사용하는데, 다익스트라가 Greedy + DP를 사용하였다면, Bellman-Ford 알고리즘은 모든 경우의 수를 탐색하는 브루트포스 방식을 사용한다는 것이다.
각 간선들을 돌면서 최단 경로에 대한 가중치를 갱신하는데 이를 노드의 수만큼 반복하여 다시 검사를 수행한다. 이렇게 한다면 음수 가중치로 인해 최종적으로 더 적어진 가중치도 잘 갱신될 수 있게 할 수 있다.
다익스트라와 동일하게, 최소 경로 가중치를 저장하는 DP-Table인 $D$를 만들 것이다.
아래와 같은 그래프가 있다고 하자
시작을 1부터 시작할 것이다. 모든 간선에 대하여 갱신이 시도된다.
$E_{12}$의 경우 $D[2] = \min(D[2], D[1] + W_{12})$에서 $D[2] = \min(\infty, 3)$이기 때문에 3로 갱신이 수행된다.
$E_{13}$의 경우 $D[3] = \min(D[3], D[1] + W_{13})$에서 $D[3] = \min(\infty, 2)$이기 때문에 2로 갱신이 수행된다.
$E_{14}$의 경우 $D[4] = \min(D[4], D[1] + W_{14})$에서 $D[4] = \min(\infty, 7)$이기 때문에 7로 갱신이 수행된다.
$E_{24}$의 경우 $D[4] = \min(D[4], D[2] + W_{24})$에서 $D[4] = \min(7, 6)$이기 때문에 6으로 갱신이 수행된다.
$E_{34}$의 경우 $D[4] = \min(D[4], D[3] + W_{34})$에서 $D[4] = \min(6, 4)$이기 때문에 4로 갱신이 수행된다.
$E_{41}$의 경우 $D[1] = \min(D[1], D[4] + W_{12})$에서 $D[1] = \min(0, 4)$이기 때문에 갱신이 수행되지 않는다
$E_{43}$의 경우 $D[3] = \min(D[3], D[4] + W_{43})$에서 $D[3] = \min(2, 3)$이기 때문에 갱신이 수행되지 않는다
$E_{45}$의 경우 $D[5] = \min(D[5], D[4] + W_{45})$에서 $D[5] = \min(\infty, 11)$이기 때문에 11로 갱신이 수행된다.
$E_{54}$의 경우 $D[4] = \min(D[4], D[5] + W_{54})$에서 $D[4] = \min(4, 6)$이기 때문에 갱신이 수행되지 않는다
여기서는 모든 간선이 문제 없이 탐색이 수행되었지만, 만약 몇몇 간선의 순서가 바뀌어 최단 경로 가중치가 $\infty$로 설정된 곳이라면 연산해도 갱신이 수행되지 않기 때문에 건너띄어야 할 것이다.
해당 알고리즘의 방식을 사용한 결과는 아래와 같다.
한 번만 수행하면 문제가 생기는 방식이지만 모든 노드의 수만큼 반복하기 때문에 결론적으로 모든 노드들에 대한 최단 경로가 계산되어 저장되게 된다. 이를 구현한 코드는 아래와 같다.
// 알고리즘 - 최단 경로 알고리즘
// 벨만-포드
public class Main {
static class Edge{
int from;
int to;
int weight;
Edge(int from, int to, int weight){
this.from = from;
this.to = to;
this.weight = weight;
}
}
public static void bellmanFord(int v, int e, int[][] data, int start) {
Edge[] edge = new Edge[e];
for (int i = 0; i < e; i++){
edge[i] = new Edge(data[i][0], data[i][1], data[i][2]);
}
int[] dist = new int[v + 1];
for (int i = 1; i < v + 1; i++){
dist[i] = Integer.MAX_VALUE;
}
dist[start] = 0;
boolean isMinusCycle = false;
for (int i = 0; i < v + 1; i++){
for (int j = 0; j < e; j++){
Edge cur = edge[j];
if (dist[cur.from] == Integer.MAX_VALUE){
continue;
}
if (dist[cur.to] > dist[cur.from] + cur.weight){
dist[cur.to] = dist[cur.from] + cur.weight;
if (i == v){
isMinusCycle = true;
}
}
}
}
if (isMinusCycle){
System.out.println("Minus cycle occurred");
return;
}
for (int i = 1; i < v + 1; i++){
if (dist[i] == Integer.MAX_VALUE){
System.out.print("INF ");
} else{
System.out.print(dist[i] + " ");
}
}
System.out.println("");
}
public static void main(String[] args) {
// Test code
int[][] data = {{1, 2, 8}, {1, 3, 6}, {1, 5, 5}, {2, 3, -5}, {2, 4, 1}, {2, 6, 4}, {3, 4, 4}, {4, 7, 3}, {5, 6, 5}, {6, 2, 0}, {6, 7, -7}};
bellmanFord(7, 11, data, 1);
data = new int[][]{{1, 2, 8}, {1, 3, 6}, {1, 5, 5}, {2, 3, -5}, {2, 4, 1}, {2, 6, 4}, {3, 4, 4}, {4, 7, 3}, {5, 6, 5}, {6, 2, -5}, {6, 7, -7}};
bellmanFord(7, 11, data, 1);
}
}
음수 사이클 문제
아래와 같은 유향 그래프가 존재한다고 가정하자
여기서 Bellman - Ford 알고리즘을 적용해보자. 1에서부터 시작한다.
$E_{12}$은 $D[2] = \min(D[2], D[1] + W_{12})$에서 $D[2] = \min(\infty, 7)$이기 때문에 7로 갱신이 일어난다.
$E_{13}$은 $D[3] = \min(D[3], D[1] + W_{13})$에서 $D[3] = \min(\infty, 6)$이기 때문에 6로 갱신이 일어난다.
$E_{23}$은 $D[3] = \min(D[3], D[2] + W_{23})$에서 $D[3] = \min(6, 5)$이기 때문에 5로 갱신이 일어난다.
$E_{31}$은 $D[1] = \min(D[1], D[3] + W_{31})$에서 $D[1] = \min(0, -2)$이기 떄문에 -2로 갱신이 일어난다.
2번째로 다시 각 노드를 순회한다.
$E_{12}$은 $D[2] = \min(D[2], D[1] + W_{12})$에서 $D[2] = \min(7, 5)$이기 때문에 5로 갱신이 일어난다.
$E_{13}$은 $D[3] = \min(D[3], D[1] + W_{13})$에서 $D[3] = \min(5, 4)$이기 때문에 4로 갱신이 일어난다.
$E_{23}$은 $D[3] = \min(D[3], D[2] + W_{23})$에서 $D[3] = \min(4, 3)$이기 때문에 3로 갱신이 일어난다.
$E_{31}$은 $D[1] = \min(D[1], D[3] + W_{31})$에서 $D[1] = \min(-2, -10)$이기 떄문에 -10로 갱신이 일어난다.
3번째도 다시 모든 데이터가 갱신될 것이다. 문제는 어딘가에서 음수 가중치로 인해 최단 거리가 계속 갱신되기 때문에 노드의 수만큼 갱신을 시켜도 다시 갱신이 수행되어야 한다는 문제점이 생긴다. 즉, 최단 경로가 고정되지 않고 계속해서 갱신되어야 하는 문제가 생긴다.
이는 어떤 노드 $V_i$에서 다른 노드 $V_j$로 가는 간선의 가중치 $W_{ij}$와 그 역으로 가는 가중치 $W_{ji}$가 있을 때 $W_{ij} + W_{ji} < 0$인경우 발생한다. 이를 음수 사이클이라고 하며 이러한 구조가 존재하는 경우에 최단 경로를 구할 수 없다.
Bellman - Ford는 이를 검출하기 위해 간단한 방식을 사용하는데 모든 노드의 수만큼 반복하는게 아닌 모든 노드의 수 + 1만큼 반복하여 마지막 검증에서 최단 경로의 값 $D[i]$가 변경되는지를 확인하는 방식을 취한다.
위의 isMinusCycle이 검증하는 용도의 변수임을 감안하고 보도록 하자.
Bellman - Ford의 시간복잡도
Bellman - Ford의 시간복잡도는 일반적으로 $O(VE)$이다. 이는 당연하게도 모든 간선을 모든 노드의 수만큼 반복하여 검사하는것이기 떄문에 산출되는 시간복잡도이다.
일반적으로 $V \leq E$ 이기 때문에 $O(V^2)$보다 큰 복잡도이며 이러한 문제로 음수 가중치가 존재하지 않는다면 다익스트라를 사용하게 된다.