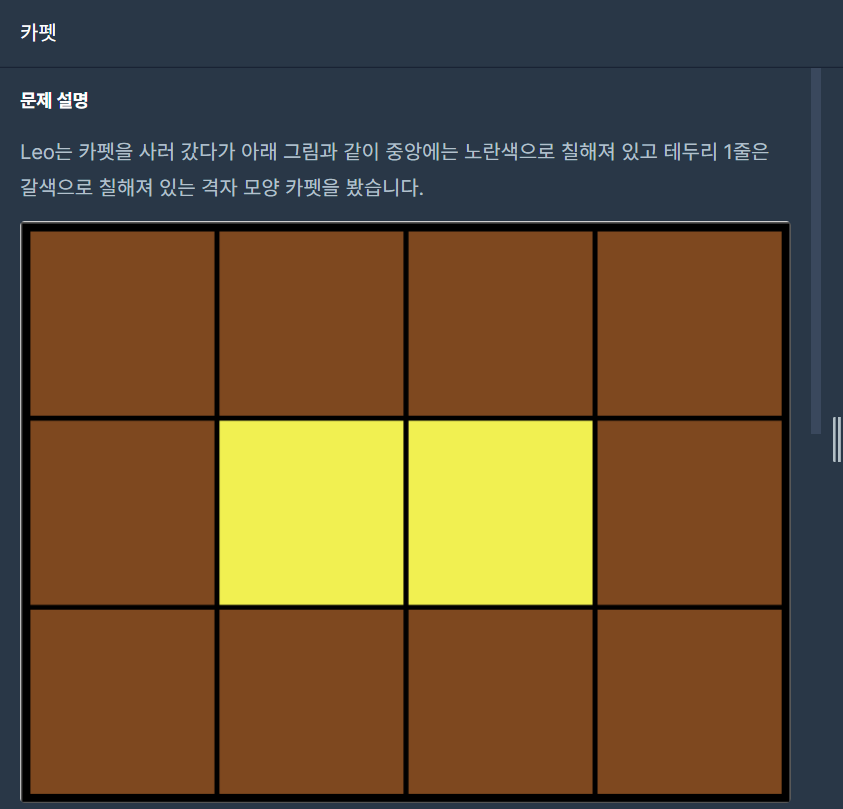
문제 설명


접근 방법
- 그림을 유심히 보면 다음과 같은 특성을 얻을 수 있다.
- 둘레에 놓인 갈색의 가로는 노란색의 가로 + 2와 같다.
- 둘레에 놓인 갈색의 세로는 노란색의 세로와 같다.
- 다만 노란색이 항상 1 x w의 형식으로 놓이지는 않기 때문에 노란색이 배치될 수 있는 경우의 수를 찾아야한다.
- 노란색의 영역이 w x h 일때 w, h이 될 수 있는 조건은 노란색의 개수의 약수여야 한다는 것에 포인트를 맞추어야 한다. 그렇다면 w, h은 다음과 같이 될 수 있을 것이다.
| W | H |
| 1 | 24 |
| 2 | 12 |
| 3 | 8 |
| 4 | 6 |
| 6 | 4 |
| 8 | 3 |
| 12 | 2 |
| 24 | 1 |
- 이때 문제에서 카펫의 가로 길이 w는 세로 길이 h 보다 크거나 같다는 조건을 본다면 경우의 수가 반토막이 난다.
- 따라서 최종적으로 생각해볼 수 있는 w, h는 다음과 같을 것이다.
| W | H |
| 24 | 1 |
| 12 | 2 |
| 8 | 3 |
| 6 | 4 |
- 이제 남은 것은 갈색의 개수를 노란색의 영역에서부터 계산해 입력으로 받은 갈색의 개수와 동일한지 검증하는 것이다. 위에서 갈색의 가로 세로 규칙과 타일의 개수를 수식화하면 다음과 같다.
$$ W_{brown} = W_{yellow} + 2 $$
$$ H_{brown} = H_{yellow} $$
$$ T_{brown} = 2\left (W_{brown} + H_{brown} \right ) $$
- 이후 갈색의 개수인 T가 입력으로 주어진 값과 동일한지 검증한다. 만약 맞다면 갈색의 가로의 길이와 갈색의 세로의 길이 + 2를 answer 배열에 넣어주면 끝이다.
답안 코드
def solution(brown, yellow):
answer = []
yellow_size_height = []
yellow_size_width = []
for i in range(1, int(yellow ** 0.5) + 1):
if yellow % i == 0:
yellow_size_height.append(i)
yellow_size_width.append(yellow // i)
for i in range(len(yellow_size_height)):
brown_width = yellow_size_width[i] + 2
brown_height = yellow_size_height[i]
if (brown_width * 2) + (brown_height * 2) == brown:
answer.append(brown_width)
answer.append(brown_height + 2)
return answer'Algorithm > BruteForce' 카테고리의 다른 글
| [백준][BOJ] 27958 사격 연습 (0) | 2023.04.06 |
|---|---|
| [BOJ 18428] 감시 피하기 (0) | 2022.12.10 |
| [Programmers] 전력망을 둘로 나누기 - python (1) | 2022.11.23 |
| [Programmers] 모의고사 - python (0) | 2022.11.22 |
| 완전 탐색의 접근방법과 사용할 수 있는 방법들 (1) | 2022.11.22 |