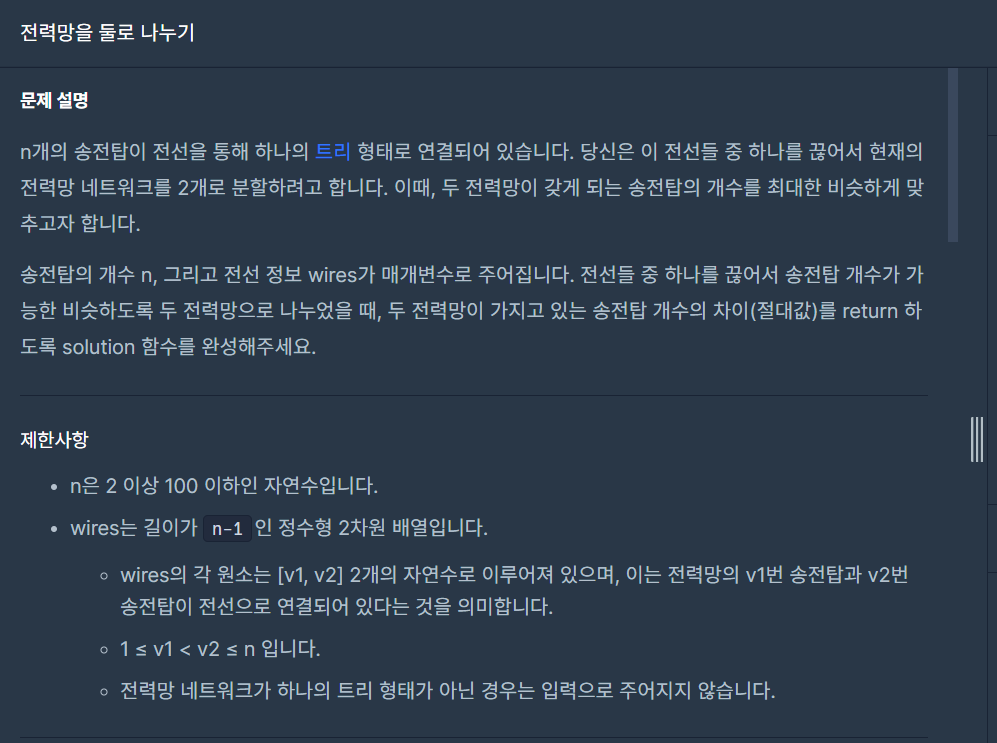
1. 문제


2. 접근 방법
- 문제의 유형이 일반적인 완전 탐색과는 달라보인다. 이 문제는 완전 탐색의 개념 + DFS/BFS 알고리즘이 합쳐진 문제로 개인적으로 꽤 좋은 문제라고 생각한다.
- 전선들 중 하나를 끊어 둘로 나뉘어진 송전탑의 개수를 구해야 한다. 이번 문제를 그래프로 모델링해보면 아래와 같을 것이다. 입력 예제로는 첫번째 샘플 예제를 사용한다.

- 이 그래프에서 우리는 어떤 간선을 잘라 두 개의 트리로 만들고 각 트리에 속한 정점의 개수들을 계산해야 한다. 간선은 단 한번만 자를 수 있다.
- 그럼 여기서 생각할 수 있는 경우의 수는 몇 가지일까? 이 문제의 경우의 수는 조합으로 환원할 수 있다
- 정점의 수가 N개라고 할 때 간선의 수는 N - 1개라고 문제에서 정의하고 있다. 여기서 1개를 선택하는 것이므로 경우의 수는 N - 1개의 간선에서 1개의 간선을 선택하는 것으로 생각할 수 있다. 그렇다면 경우의 수는 다음과 같이 나올 것이다.
N−1C1
- 조합의 계산을 수행할 경우 위 식의 결과는 N - 1이 된다. 즉 모든 경우의 수는 N - 1가지가 된다.
- 그렇다면 '끊는다' 라는 것은 어떻게 표현해야할까? 이는 매우 간단히 표현할 수 있는데 그래프를 정의할 때 그 간선을 택해서 무시하면 된다.
- 위 과정들을 통해 우리는 이제 이 모든 경우의 수에 대한 그래프를 나타낼 수 있다. 이제 남은건 나눠진 각 트리(그래프)에 속한 정점의 수가 몇 개 인지를 추려내는 것이다.
- 이 과정은 DFS/BFS의 그래프 탐색으로 구할 수 있으며 이 둘의 차의 절댓값을 구하고 이중 최소의 경우를 answer에 나타내면 끝이다.
3. 답안 코드
# 그래프에 속한 정점의 개수
node_cnt = 1
# 나누어진 그래프들 각각에 대해 DFS로 해당 그래프에 속한 정점의 개수를 계산한다
def dfs(graph, v, visited):
global node_cnt
for nv in graph[v]:
if not visited[nv]:
node_cnt += 1
visited[nv] = True
dfs(graph, nv, visited)
def solution(n, wires):
global node_cnt
answer = 1e9
# 모든 경우의 수에 대해서 그래프를 모델링한다.
# 여기서는 i번째 경우의 수를 wires의 i번째 간선을 끊는것으로 표현했다.
for i in range(n - 1):
graph = [[] for _ in range(n + 1)]
visited = [False for _ in range(n + 1)]
nodes = []
for w in range(len(wires)):
# 만약 그래프의 i번째 간선이라면 해당 간선은 무시한다.
if w == i:
continue
v1, v2 = wires[w]
graph[v1].append(v2)
graph[v2].append(v1)
# 이후 모델링된 그래프를 DFS을 통해 정점의 개수를 구한다
for j in range(1, n + 1):
if not visited[j]:
visited[j] = True
node_cnt = 1
dfs(graph, j, visited)
nodes.append(node_cnt)
diff = abs(nodes[0] - nodes[1])
answer = min(answer, diff)
return answer- 이 문제는 답을 적절히 바꾸는 것으로 다른 문제로 만들 수 있다. 예를 들자면 1개를 끊는게 아닌 임의의 수 x 개를 끊어 각각의 정점의 개수 중 최대값을 구하게도 할 수 있을 것이다.
- 만약 그런 경우 나올 수 있는 그래프의 경우의 수는 몇 가지일까? 접근 방법을 잘 생각해보면 금방 도출해낼 수 있을 것이다.
'Algorithm > BruteForce' 카테고리의 다른 글
| [백준][BOJ] 27958 사격 연습 (0) | 2023.04.06 |
|---|---|
| [BOJ 18428] 감시 피하기 (0) | 2022.12.10 |
| [Programmers] 카펫 - python (1) | 2022.11.23 |
| [Programmers] 모의고사 - python (0) | 2022.11.22 |
| 완전 탐색의 접근방법과 사용할 수 있는 방법들 (1) | 2022.11.22 |