1. 최소 신장 트리 문제
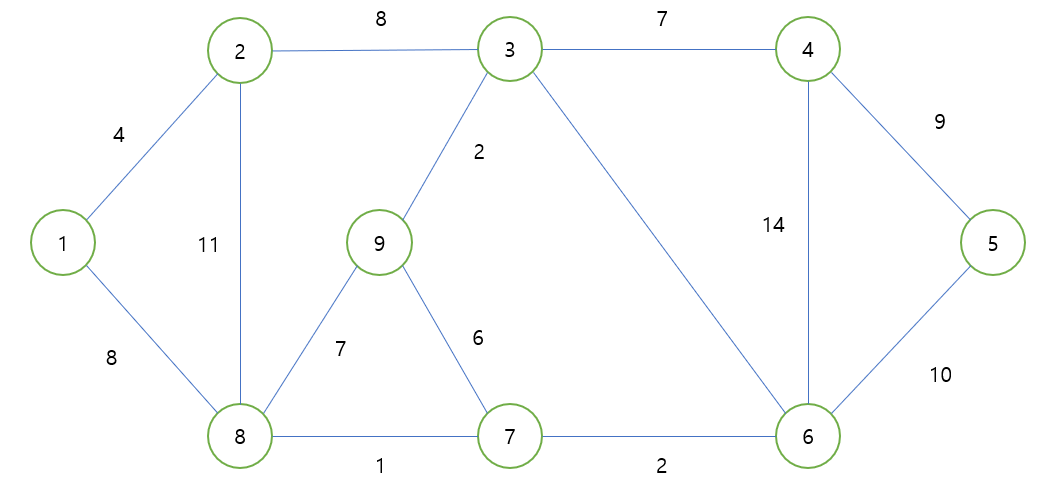
- 아래와 같은 그래프가 있다고 가정하자.

- 각각의 노드를 도시로, 간선을 도로로 생각해보자. 우리는 정부에서 예산을 받아 해당 도시들을 모두 이어주는 도로들을 만들어야 한다. 지금 주어진 간선들은 도로 후보군들로, 각 도로를 건설하는데 드는데 소비되는 예산이 표시되어있다.
- 언제나 예산은 부족하기 때문에 우리는 최소의 비용으로 모든 도시를 이어줄 수 있도록 하는 도로 후보군들을 뽑아야 한다. 이때, 드는 예산의 최소값은 얼마인가?
- 이것에 대한 정답은 아래와 같이 간선을 연결하는 경우이며, 총 예산은 37이 된다.

- 이때 진하게 칠해져 있는 노드들과 간선의 집합을 통틀어 최소 신장 트리(Minimum Spanning Tree - MST)라고 부른다.
2. MST의 정의
- MST의 정의는 심플하게 설명하면 아래와 같다.
- 어떤 무방향 가중치 그래프 G(V,E)가 존재할 때, 다음과 같은 간선 E의 부분집합 T가 존재한다.
- T에 속한 간선들에 의해 그래프의 모든 정점이 서로 연결된다.
- 이때 각 간선 (u,v)∈E에 대한 가중치w(u,v)의 합 즉, Σ(u,v)∈Tw(u,v) 가 최소가 되어야 한다.
- 이를 풀어서 설명하자면 무방향 가중치 그래프에서 모든 정점을 연결하면서, 동시에 그 가중치의 합이 최소가 되는 간선의 집합을 MST라고 한다.
- 그렇다면 왜 Tree 인가? 라는 생각을 할 수 있다. 이는 사실 가중치의 합이 최소가 된다 라는 관점에서 살펴보면 너무나 당연한 의미가 된다.
- Tree의 정의는 사이클이 없는 무방향 그래프로 정의할 수 있다.
- 그렇다면 먼저 Tree일 필요가 없다고 가정해 보자 즉, 가중치의 합이 최소가 되는 그래프가 존재하고, 이 그래프 내부에 사이클이 존재한다는 가정을 해보자.
- 이는 모든 정점이 연결되어 있는 동시에 가중치의 합이 최소가 되는 그래프이다. 그런데 생각해 보면 사이클이 만들어지면, 하나의 정점에서 다른 정점으로 가는 길이 2가지가 된다는 것이다.
- 이는 곧 두 가지 길 중 하나를 끊어도, 즉 두 개의 간선 중 하나를 삭제시켜도, 모든 노드가 연결된다는 조건은 만족된다. 동시에 두 개의 간선 중 하나를 삭제하기 때문에, 가중치의 합이 그만큼 줄어든다. 즉, 사이클을 이루는 간선 중 하나를 삭제함으로서 모든 정점이 연결되는 동시에 가중치의 합이 더 최소가 되는 그래프가 완성되었다.
- 이는 맨 처음 "가중치의 합이 최소가 되는 그래프가 존재하고, 이 그래프 내부에 사이클이 존재한다" 라는 가정과 모순된다. 따라서 사이클이 존재하지 않아야 한다는 것이 참으로 증명되었다.
- 이때 그래프 내부에 사이클이 존재하지 않으므로, 해당 그래프 구조는 곧 Tree라고도 할 수 있다.
3. MST 알고리즘
3.1. Generic MST 알고리즘
- 최소 신장 트리를 찾는 알고리즘은 여러 가지가 존재하나 공통적인 알고리즘은 아래와 같은 순서로 이루어진다.
- 먼저 A=∅ 인 집합을 선언한다.
- 이 집합 A에 대해 안전한 간선을 하나 찾은 후, 이를 A에 더한다(Union)
- A에 속한 에지의 개수가 N−1개가 될 때 까지 2번을 반복한다.
- 알고리즘은 매우 심플해보인다. 하지만 "안전한" 이라는 것의 정의를 아직 내리지 않았다. 이것에 대하여 먼저 살펴보아야 해당 알고리즘을 이해할 수 있을 것이다.
- 위에서 말한 "안전한"의 의미는 아래와 같다.
- 어떤 MST의 부분집합 A에 대하여 A∪{(u,v)}를 수행할 때 그 결과 역시 어떤 MST의 부분집합이 될 때 이 간선 E(u,v)가 A에 대하여 안전하다(safe) 라고 정의한다.
3.2. Find Safe Edge
- 이제 안전한 간선이 어떤 것인지를 알아봤으니 이 안전한 간선을 어떻게 찾을 것인가에 대하여 고민해보아야 한다.
- 이를 알아보기 위해서 다음과 같은 용어를 사용할 것이다.
- 어떤 그래프 G=(V,E)가 있을 때, 그래프의 정점들을 두 개의 집합 S와 V−S로 분할한 것을 컷 (S,V−S)라고 부른다.
- 어떠한 간선 E(u,v)에 대하여, u∈S이고, v∈(V−S)일 때 E(u,v)는 컷 (S,V−S)를 cross한다 라고 정의한다.
- 간선들의 부분집합 A에 속한 어떤 간선도 컷 (S,V−S)를 cross 하지 않을 때 컷 (S,V−S)는 간선들의 부분집합 A를 존중한다(respect)라고 정의한다.
- 글로만 보면 이해가 힘들어 보인다. 그림을 예시로 들어 한번 위의 개념들을 알아보자

- 이때 정점의 집합 V는 그래프에 있는 모든 정점을 모은 집합으로 정의된다.
- 아래 사진과 같이 V에 대한 부분 집합 S를 설정하였다. 그럼 S에 포함되지 않은 모든 정점은 자연스럽게 (V−S)로 포함될 것이다.

- 이렇게 분리된 상황 이 자체를 앞으로 컷 (S,V−S)라고 정의한다.
- 위 그림에서 간선 E(b,c)와 E(f,e)를 살펴보자 b,f∈S이고, c,e∈(V−S)이다. 즉 이 집합 사이를 교차하고 있다는 것이다. 이것을 이제 간선 E(b,c), E(f,e)가 컷 (S,V−S)를 크로스(cross)한다 라고 정의한다.
- 어떤 MST의 부분집합 A가 존재한다고 가정한다. A={E(a,b),E(a,f),E(d,c),E(d,e)} 라고 하자. 아래 그림에서는 굵은 간선이 부분집합 A에 포함된 간선이 될 것이다.
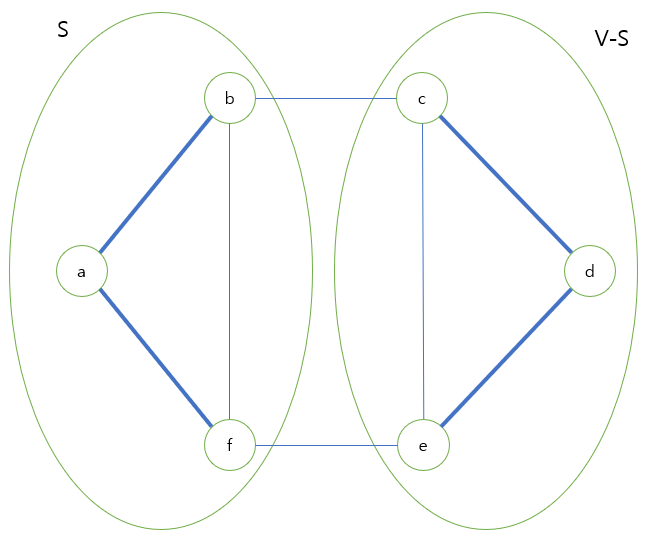
- A={E(a,b),E(a,f),E(d,c),E(d,e)} 인 간선들을 잘 살펴보자. A에 포함된 어떤 간선도, 컷 (S,V−S)를 크로스하지 않는다는 것을 알 수 있다.우리는 이를 집합 A가 컷 (S,V−S)을 존중한다(respect)라고 할 것이다.
- 위의 장황한 설명과 예시를 통해 용어들의 정리를 마쳤다.이 용어들이 왜 필요한지는 다음 글에서 다루도록 하겠다.
'Algorithm > MST' 카테고리의 다른 글
| [Disjoint Set] BOJ 25579 터트려라 풍선 (0) | 2023.04.23 |
|---|---|
| 최소 신장 트리(Minimum Spanning Tree) - 5 (0) | 2023.04.09 |
| 최소 신장 트리(Minimum Spanning Tree) - 4 (0) | 2023.04.09 |
| 최소 신장 트리(Minimum Spanning Tree) - 3 (0) | 2023.04.08 |
| 최소 신장 트리(Minimum Spanning Tree)- 2 (0) | 2023.04.08 |