최소 신장 트리(Minimum Spanning Tree) - 1
최소 신장 트리 문제 아래와 같은 그래프가 있다고 가정하자. 각각의 노드를 도시로, 간선을 도로로 생각해보자. 우리는 정부에서 예산을 받아 해당 도시들을 모두 이어주는 도로들을 만들어야
sehun5515.tistory.com
지금까지의 내용 요약
- 최소 신장 트리는 어떤 무방향 가중치 그래프가 주어졌을 때, 그 그래프의 모든 정점을 연결하면서, 가중치의 합이 최소가 되는 간선의 부분집합으로 정의했다.
- 최소 신장 트리를 구하는 Generic한 알고리즘은 아래와 같은 과정을 거친다.
- 먼저 $A = \emptyset$ 인 집합을 선언한다.
- 이 집합 $A$에 대해 안전한 간선을 하나 찾은 후, 이를 $A$에 더한다(Union)
- $A$에 속한 간선의 개수가 $N - 1$개가 될 때 까지 2번을 반복한다.
- 이때 "안전하다(safe)" 라는 개념을 아래와 같이 정의했었다.
- 어떤 MST의 부분집합 $A$에 대하여 $A \cup \{(u, v)\}$를 수행할 때 그 결과 역시 어떤 MST의 부분집합이 될 때 이 간선 $E(u, v)$가 $A$에 대하여 안전하다(safe) 라고 정의한다.
- 그리고 이 "안전한"간선을 찾기 위해서 필요한 정리를 알아보기 위해 용어 정리를 수행하였다. 각 용어의 정의는 아래와 같다.
- 어떤 그래프 $G = (V, E)$가 있을 때, 그래프의 정점들을 두 개의 집합 $S$와 $V-S$로 분할한 것을 컷 $(S, V-S)$라고 부른다.
- 어떠한 간선 $E(u, v)$에 대하여, $u \in S$이고, $v \in (V-S)$일 때 $E(u, v)$는 컷 $(S, V-S)$를 cross한다 라고 정의한다.
- 간선들의 부분집합 $A$에 속한 어떤 간선도 컷 $(S, V-S)$를 cross 하지 않을 때 컷 $(S, V-S)$는 간선들의 부분집합 $A$를 존중한다(respect)라고 정의한다.
Find safe edge
- 위의 용어를 숙지한 상태에서 다음과 같은 정리가 성립한다.
- 임의의 컷 $(S, V-S)$가 존재하고 이 임의의 컷이 어떤 MST의 부분집합 $A$를 respect 할 때, 컷 $(S, V-S)$를 cross하는 간선 중 그 가중치가 가장 적은 간선은 $A$에 대해 safe하다
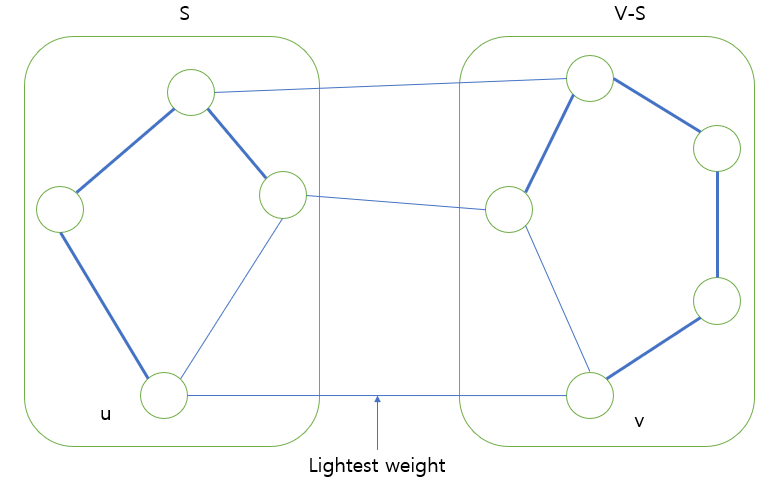
- 역시나 글로만 봐선 이해하기가 힘들다. 그림을 통해 알아보도록 하자 아래와 같은 그래프와 컷 $(S, V-S)$가 존재한다고 생각하자. 여기서 진한 간선은 어떤 MST의 부분집합 $A$를 의미한다.

- 그림을 잘 보면 $A$에 속한 어떤 간선도 컷 $(S, V-S)$를 cross하지 않는다는 사실을 알 수 있다. 즉, 해당 컷은 $A$를 respect한다.
- 이때 컷 $(S, V-S)$를 cross하는 간선들을 살펴보자. 이 간선들 중 가장 가중치가 적은 간선 즉 맨 아래에 화살표가 가리키고 있는 간선은 $A$에 대해 safe 하다는 것이 위의 정리의 내용이다.
정리의 증명
- 정리에 대해서 설명을 통해 알았지만 "왜" 이 정리가 성립하는지는 아직 모른다. 이제 위의 정리를 증명해서 왜 컷을 크로스하는 간선 중 가장 가중치가 가벼운 간선이 safe한가를 알아볼 것이다.
- 먼저 해당 정리를 반박하는 가설을 새워보자. 가설은 다음과 같다.
- 어떤 MST의 부분집합 $A$가 존재한다. 단, 해당 부분집합 $A$는 가장 적은 가중치를 가진 간선 $E(u, v)$를 포함하지 않는다. 즉 MST의 내부에서 간선 $E(u, v)$는 존재하지 않는다.
- 해당 가설이 모순이라는 것을 증명하면, 해당 정리가 참이라는 것이 증명된다.(proof by contradiction)
- 이제 해당 가설에 대해 분석해보자. $A$가 어떤 MST의 부분집합이라고 가정하였으므로, $A$에 속한 간선들을 모두 포함하는 MST가 존재한다는 것을 알 수 있다.
- 즉 위의 사진에서 정점 $u$, $v$가 가장 가중치가 적은 간선 $E(u, v)$를 통하지 않고도, 서로 연결되어 있다는 것이 보장된다.
- 그런데 $u \in S$, $v \in (V-S)$이기 때문에 $u$에서 $v$로 가는 경로는 최소한 한 번은 해당 컷을 크로스해야하는 것이 자명하다.

- 위의 사진과 같이, $E(u, v)$가 아닌 $E(x, y)$를 통해 연결되어도, MST가 존재한다고 말할 수 있을 것이다. 여기서 컷 $(S, V-S)$를 크로스하는 간선 $E(x, y)$의 가중치는 $E(u, v)$보다 같거나 크다. 즉 $w(u, v) \leq w(x, y)$이다.
- 이는 매우 자명한 사실이다. 왜냐면 위의 가정에서부터 가장 가벼운 간선이 $E(u, v)$라고 정했기 때문이다.
- 그렇다면, 이제 해당 MST에서 간선 $E(x, y)$를 선택하지 않고, 간선 $E(u, v)$를 선택했다고 가정해 보자.
- 그렇다면 전체적인 가중치 합은 간선 $E(x, y)$를 선택했을때에 비해서 적어도 커지진 않을 것이다. 왜냐하면 위에서 알아봤듯 $w(u, v) \leq w(x, y)$ 가 성립되어 있기 때문이다.
- 그렇다는 말은 $E(x, y)$를 빼고, $E(u, v)$를 선택하였을 때, 모든 노드가 연결되어 있다는 것이 증명된다면, $E(u, v)$를 포함하는 MST가 존재한다는 것이 되므로 가설에 모순이 생기면서 증명이 완료될 것이다.
- 이를 증명하기 위해 임의의 정점 $s$, $t$를 각각 $S$와 $(V-S)$에 넣어볼 것이다.

- 두 정점 $s$, $t$가 $E(x, y)$를 거치지 않고 연결되어 있다면, 간선 $E(x, y)$를 제거한다고 해서 두 정점의 연결이 끊어지지 않는다. 이것은 매우 자명한 사실이다.
- 그렇다면 $s$ $t$가 $E(x, y)$를 통해 연결되어 있는 경우에는 어떨까

- 위의 그림에서 간선 $E(x, y)$를 제거하고, $E(u, v)$를 연결시킨다고 가정하자.
- 그림을 보면 알겠지만 $E(x, y)$를 뺌으로서 다이렉트로 이어지진 않아도, $E(u, v)$를 선택함으로 인해서 다음과 같은 경로로 $s$, $t$가 연결되는 것이 보장된다.
- $E(s, x)$ -> $E(x, u)$ -> $E(u, v)$ -> $E(v, y)$ -> $E(y, t)$
- 따라서 $E(x, y)$를 거치지 않아도(제거하여도) 임의의 두 정점이 연결되어 있다는 것이 증명되었다.
- 이때 위에서 서술하였듯 $E(x, y)$를 제거하고 $E(u, v)$를 넣었을 때의 가중치의 합은 $E(x, y)$를 넣은 가중치의 합보다 크지 않으므로 모든 정점을 연결하면서 그 가중치가 최소가 되는 부분집합이라는 최소 신장 트리의 정의를 만족한다.
- $E(u, v)$ 가 MST에 포함되는 경우가 생기기 때문에, 어떤 MST의 부분집합 $A$가 존재하고, $A$는 간선 $E(u, v)$가 존재하지 않는다 라는 가정에 모순이 발생한다. 따라서 정리가 참으로 증명되었다.
정리하며
- 지금까지 MST의 일반적인 알고리즘을 살펴보고, 알고리즘에 사용되는 용어의 정리와, 그에 따른 정리를 알아보았고, 해당 정리의 증명도 완료하였다.
- 다음 글부터는 MST의 일반적인 알고리즘을 좀더 세부적으로 구현시킨, Kruskal알고리즘, Prim알고리즘에 대해서 알아볼 것이다.
'Algorithm > MST' 카테고리의 다른 글
| [Disjoint Set] BOJ 25579 터트려라 풍선 (0) | 2023.04.23 |
|---|---|
| 최소 신장 트리(Minimum Spanning Tree) - 5 (0) | 2023.04.09 |
| 최소 신장 트리(Minimum Spanning Tree) - 4 (0) | 2023.04.09 |
| 최소 신장 트리(Minimum Spanning Tree) - 3 (0) | 2023.04.08 |
| 최소 신장 트리(Minimum Spanning Tree) - 1 (0) | 2023.04.07 |